De 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos De 16 y 74 grados Este triángulo notable es bastante sencillo de aprender por las proporciones enteras que poseeTRIÁNGULOS NOTABLES Y POR APROXIMACIÓN by JUSTO GUSTAVO INGA FLORES SECUNDARIA QUINTO AÑO 67º30 22º30 1 21 4 72º 18º 5210 78º30 11º30 1 5 26 75º 15º 26 − 26 4 67º 23º 5 12 13 8º º 1 7 3º 87º K 19K 16º 74º 7 24 25 45º 45º 1 1 2 60º 30º 1 2 3 76º 14º 1 4 17 53º 37º 3 4 5 8º 8 2º 1 0 2 27 54º 36º 15 4 1 525 72º MoreFue un filósofo y matemático griego considerado el primer matemático puro Contribuyó de manera Podemos caracterizar a un triángulo rectángulo significativa en el avance de la geometría, como notable cuando existe una relación matemática helénica, la aritmética, derivadas conocida entre sus lados

Aprender Los 9 Triangulos Rectangulos Notables
Triangulo rectangulo notable de 15 y 75
Triangulo rectangulo notable de 15 y 75-Se denomina triángulo notable a todo triángulo cuyos lados sean conocidos¿Qué es un triángulo Triángulo notable de 15° y 75° Pitágoras rectángulo notable?
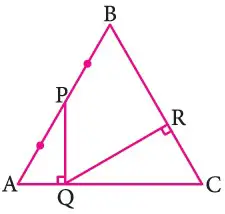



Triangulos Rectangulos Notables Y Pitagoricos Para Tercer Grado
ExplicaciónLos triángulos notables más importantes, por así decirlo, son aquellos que se ven con mayor frecuencia en soluciones de problemas en materias como la geometría, trigonometría, física y otros Los triángulos notables más conocidos son 45, 37 y 53, 60 y 30, 15 y 75, 74 y 16 Amigo02 Amigo02De 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos De 16 y 74 grados Este triángulo notable es bastante sencillo de aprender por las proporciones enteras que poseePor extensión, todas las demás líneas notables, es decir, las alturas, las medianas y las bisectrices de un triángulo son también cevianas Ceviana interior Ceviana interior BD Ceviana exterior Ceviana interior BD Ya que el punto donde recae la ceviana puede pertenecer al lado del triángulo o a su prolongación, estas se denominarán
la verdad no conosco ese triangulo dudo mucho que sea notable Para que deseas saberlo?, tarea de cole?15 Frontera y exterior Los tres lados de un triángulo constituyen su frontera y los puntos del plano que no están en el interior ni en la frontera están en el exterior del triángulo 16 La unión del interior, del triángulo (frontera) y del exterior es igual al plano del triánguloBusca cursos, habilidades y videos Contenido principal Matemáticas Trigonometría Preparación Educación Superior Razones trigonométricas en triángulos rectángulos Razones trigonométricas de ángulos agudos notables en triángulos rectángulos
A los ángulos de 30º, 45º y 60º (ó sus equivalentes en radianes π/6 rad, π/4 rad y π/3 rad) se les conoce como ángulos notablesSe llaman así porque aparecen muy a menudo en nuestra vida cotidiana, y resulta de gran utilidad aprender de memoria losCalcula ac/b de un triángulo notable de 53° C= 15° Triangulo oblicuangulo como resuelvo eso Responder victoria Marzo Si la hipotenusa de un triángulo rectángulo mide 75 y uno de sus ángulos es de 35°, se pide calcular los 2 catetos y el otro ángulo Responder sofiaÁrea del Triangulo, Angulo de 30 Grados, Circunferencia Inscrita, Incentro, Tangente Problema de Geometría 618 Área del Triangulo, Angulo de 60 Grados, Circunferencia Inscrita, Incentro, Tangente Problema de Geometría 405 Cuadrilatero, 60, 75, y 135 grados, Punto Medio Problema de Geometría 368



1
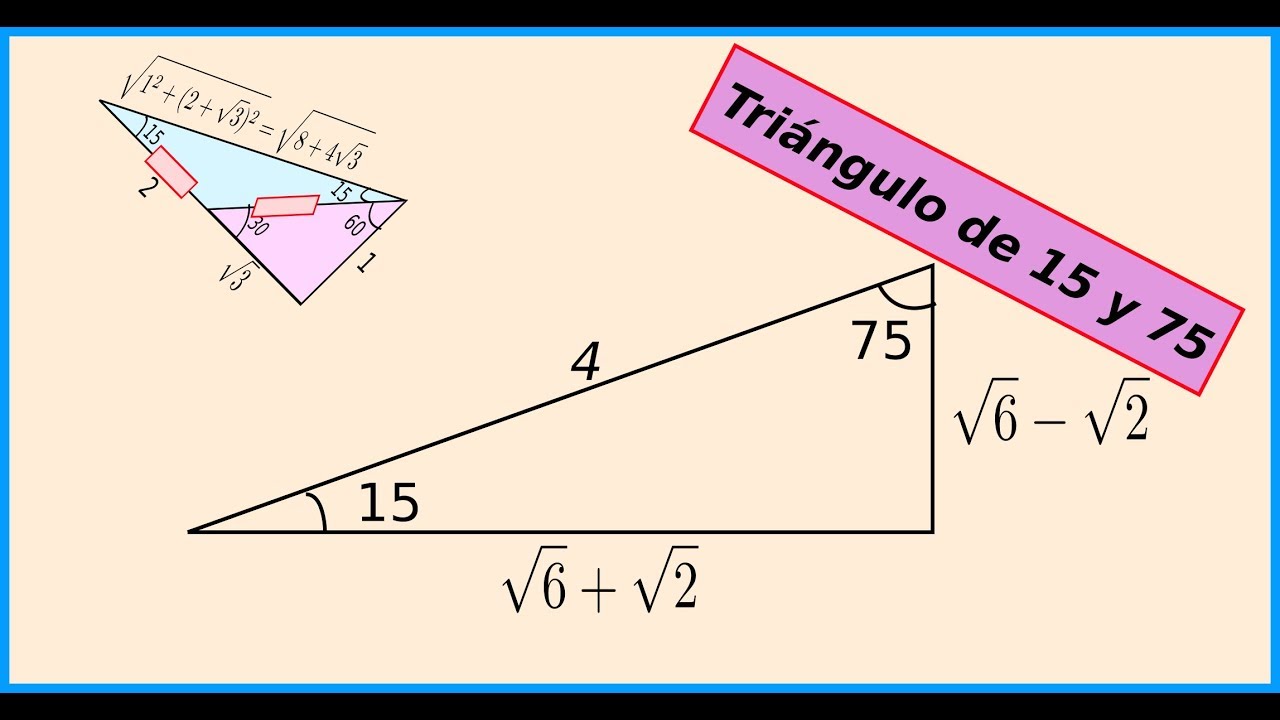



El Triangulo De 15 Y 75 Grados Youtube
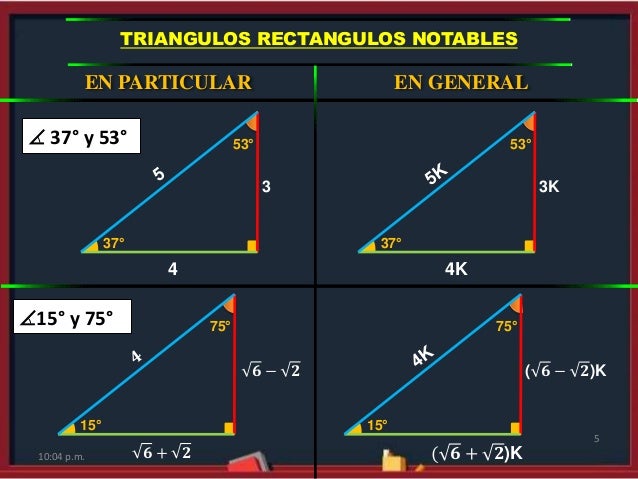
necesito informacion sobre el triangulo notable de º y 7º algunos trucos para memorizar cuanto es la tangente de 14 grados, pues el cociente de sus dos numeros 1/4 jeje ¡¡¡¡¡angulo que vino varias veces en examenes de admision!!! De 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos De 16 y 74 grados Este triángulo notable es bastante sencillo de aprender por las proporciones enteras que posee Más triángulos notables Triangulos rectangulos notables (completo) 1 TRIÁNGULOS RECTÁNGULOS NOTABLES 2k k 3k 30° 60° 5k 3k 4k 37° 53° 2k k k 45° 45° 25k 7k 24k 16° 74° 17k k 4k 14° 76° 4k ( 6 2)k 15° 75° 10k k 3k 37 2 ° 5k k 2k 5 2k k 7k 8° ° 137k 11k 4k 70° ° 61k 6k 5k 50° 40° 4k ( 5 1)k ( )10 2 5k 18° 72° 4k ( )10 2 5k ( )5 1k 36° 54° 149k 7k 10k 35°
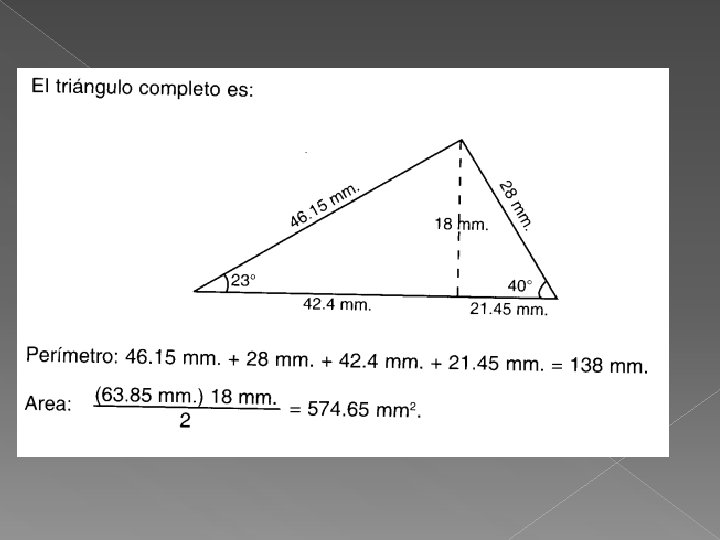



Unidad I Utilicemos Las Razones Trigonometricas Trigonometra Es




Triangulos Rectangulos Notables Matemath Web
Triángulo notable de 54° y 36° Razones trigonométricas de los triángulos notables Triángulo notable de 75° y 15° Otros Triángulos Notables ¿Qué es un triangulo notable?PeterWill, #6 kikinstone Miembro nuevo Registro Mensajes 28 Likes 1 Temas 12 facil, crea un triangulo de 37 y 53 luego haces una bisectriz del angulo 37, separas 15 grados y lugo le aumentas 2 grados del angulo 3715En un triángulo acutángulo ABC se sabe que m B = 50° D Se trazan las alturas AH y CP las cuales se cortan en "Q" Calcular "m PQH" a) 1º b) 100º c) 110º d) 130º e) 90º 16En un triángulo ABC se sabe que m B = 62° y m C = 18°




6 Triangulo Notable De 37 Y 53 Y De 45 Triangulos Rectangulos Notables Ejercicio Resuelto Cute766




Triangulos Notables De 15
El triángulo 45°45°90° es un triángulo rectángulo cuyos lados se encuentran comúnmente en la proporción Las medidas de los lados son x , x , y En un triángulo 45°45°90°, la longitud de la hipotenusa es por la longitud de un cateto Para ver porque es esto, dese cuenta que por el inverso del teorema de Pitágoras , estosK El triangulo notable de 45 y 45 53 3K El triangulo de 37 y 53 1K K50 7K El triangulo de 8 y 30 K 3 74 2K 25K 7K 16 60 1K El triangulo de 30 y 60 24K El triangulo de 16 y 74 10K 37/2 3K El triangulo de 37/2 75 4K 5 K (6 2)K K 15 53/2 (6 2)K 2K El triangulo de 15 y 75 El triangulo de 53/2 67 5K 13K 23Otros triangulos notables Otros triángulos notables no tan conocidos son El triángulo de 15 y 75 El triángulo de 18 y 72 El triángulo de 36 y 54 Publicado por Unknown en 1309




Razones Trigonometricas En Triangulos Rectangulos Video Khan Academy




Problema 434
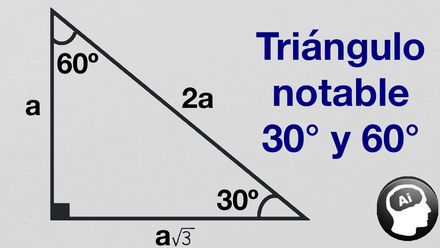
EJERCICIO 5 En el primer triangulo AFB de la izquierda HAY UN ANGULO DE 30°, ENTONCES eL OTRO ANGULO INTERNO SERA 60° En el triangulo BCE el angulo que te dan es 67°, con es dato puedes calcular el angulo del triangulo EBF(60°X67°=180°)ENTONCES X=53° Ahora en el triangulo AFB K=75;Un triángulo 30°60°90° es comúnmente encontrado como un triángulo rectángulo cuyos lados están en la proporción Las medidas de los lados son x , , y 2 x En un triángulo 30°60°90°, la longitud de la hipotenusa es dos veces la longitud del cateto más corto, y la longitud del cateto más largo es veces la longitud del cateto75° D Tres ciudades A, B y C están unidas por carreteras rectas, por motivos de presupuesto los alcaldes planean construir una estación de bomberos ubicada en el interior del triángulo ABC luego construir vías de acceso rápido desde la estación a cada una de las carreteras (lados del triángulo ABC), con la condición que sean las más



1




Triangulos Rectangulos Notables Matemath Web
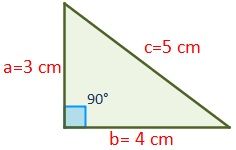
El área de un triángulo es base ( b b) por altura ( a a) divido entre 2 Como sabemos que el área es 15 c m 2 15 c m 2 y que la base es b = 6 c m b = 6 c m, podemos calcular la altura La altura del triángulo es 5cm Finalmente, calculamos la hipotenusa aplicando Pitágoras La hipotenusa mide, aproximadamente, 781cm Ejemplo Hallar la hipotenusa del siguiente triangulo sabiendo que el ángulo que se le antepone al ángulo de 37° es 9 Explicación Triangulo Notable El cateto mas pequeño es aquel que se opone al ángulo mas pequeño y así viceversa Son aquellos triángulos que a partir de la razón Triángulos notables SON Triángulos rectángulos cuyos lados son "conocidos" En Triangulo rectángulo es Un triangulo con un ángulo de 90° Usamos EL TEOREMA DE PITAGORAS para Hallar las medidas de los catetos o hipotenusa a c b Catetos BC y CA Hipotenusa AB Alfa Beta = 90° Son varios los triángulos notables conocidos La mayoría de los casos, las relaciones




Triangulo Notable De 15 Y 75 Profesorajesus Com



1
De 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos Te explicamos cómo encontrar las razones trigonométricas deángulos notablesusando el teorma dePitagorás la altura ylos ángulos deun triánguloequiláteroycalcule exactamente el valor del seno, el coseno yla tangente de30°Y son triángulos congruentes porque sus lados y ángulos correspondientes son iguales Veamos otro par de triángulos Abajo se muestran los triángulos y Estos dos triángulos no son congruentes porque es claramente más pequeño en tamaño que Pero, a pesar de que no tienen el mismo tamaño, se parecen el uno al otro Para ambos caso el triangulo notables es el triangulo recto Debemos recordar que un triangulo recto o rectángulo es aquel que tiene un angulo de 90° Así mismo, la suma de todos los ángulos internos de un triangulo debe sumar 180° En el primer caso, tenemos los angulo 10 y 80, por lo tanto 10 80 x = 180 x = 180 90 x = 90 El triangulo es recto



2
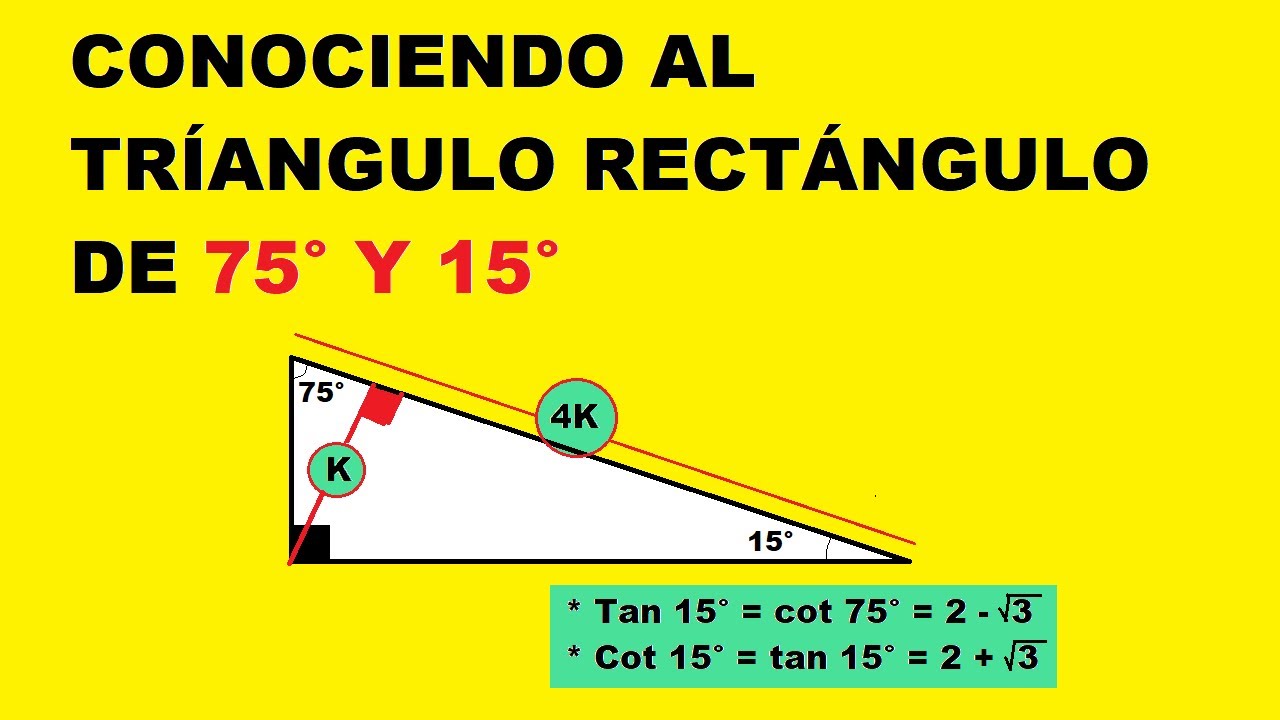



Un Interesante Triangulo Notable 75 Y 15 Conclusiones Youtube
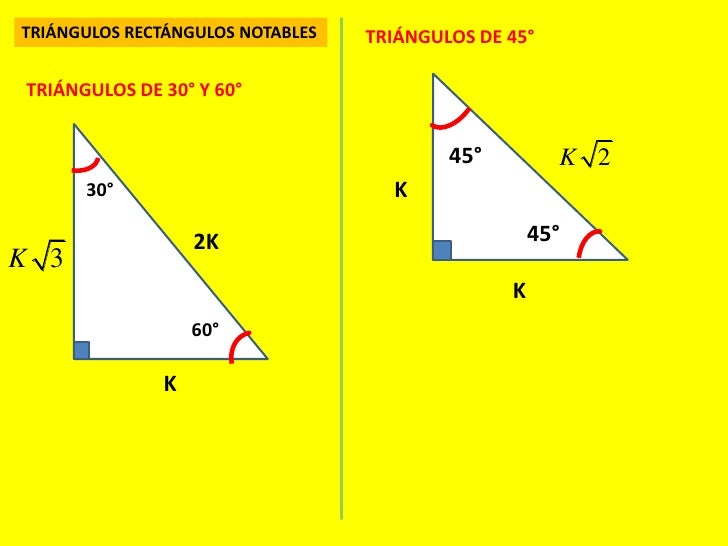
Triángulos Notables Son aquellos triángulos que a partir de la razón de dos de sus lados se pueden calcular su tercer lado y la medida de sus ángulos internos Sólo existen dos triángulos rectángulos notables de medidas exactas y son aquellos que se deducen del triángulo equilátero y del cuadrado, estos son los de 30°, 60° y de 45°Calcular E = x – y Resolución Complementamos el ángulo que falta y colocamos los lados Ahora calculamos el valor de «k» y lo reemplazamos para calcular los valores de «x» e «y» resolución En la figura adjunta, se sabe que AB = 18m, ÐCAD = 15° y el ÐCBD = 30°, calcular la longitud "CD" más ahora viendo Triángulo Notable de 15° y 75° Jesus Mendez now playing Comas Educación inicial para los niños del colegio Libertad Jesus




Triangulo Notable De 15º Y 75º Demostracion Youtube




Ejercicios De Triangulos Notables Ayudenme A Resolver Estos Ejercicios Xfa Brainly Lat
Triángulo Notable de 15° y 75° Explicación de cómo formar el Triángulo Notable de 15° y 75°http//profesorajesuscomMáster Jesús Méndez CollantesFacebookTriangulo de 16 y 74 Crea una Clase15°, 30°, 45° y 60° En base a ésta información, uno puede calcular en forma exacta, los valores de las funciones seno y coseno cada 15° Analizando el primer cuadrante, tenemos los valores exactos de 15°, 30°, 45°, 60° y 75° Hay que notar que para el ángulo de 75°, puede ser generado por la suma de 30° más 45°



Triangulo Rectangulo




Todo Los Triangulos Notables Sus Angulos Medidas
En la figura, ABCD es un trapecio, las áreas de las regiones triangulares ABD y BCD son 75 cm2 y 50 cm2 respectiva mente Halle el área de la región triangu larEl estilo se define en los pequeños detalles ES NOTABLE POR Su discreto diseño en forma de triángulo Distinguirse sin llamar la atención Es un símbolo de distinción a la hora de organizar tus papeles ESTILO RETRO NORDICO La marca danesa Monograph ofrece elementos esenciales para el emprendedor y el creativo ElemeDe 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos De 16 y 74 grados Este triángulo notable es bastante sencillo de aprender por las proporciones enteras que posee Más triángulos notables Triángulo notable de 37/2 grados Triángulo notable de 53/2 grados Razones




El Cerebrito Importantes Triangulos Rectangulos Notables Facebook




Triangulos De 30 Y 60 45 Y 45 37 Y 53 Razones Trigonometricas Notables Ejercicios Res Razones Trigonometricas Ejercicios Resueltos Formulas Matematicas
Podemos caracterizar a un triángulo como notable cuando existe una relación conocida entre sus lados En la mayoría de los casos, las relaciones entre sus lados se limitan a número enteros o número irracionales Los triángulos notables más conocidos son El triangulo notable de 45 y 45 El triangulo de 30 y 60 El triangulo de 37 y 53ADMISIÓN 112 CON GRUENCIA DE TRIÁNGULOS Ademas observaremos que el triángulo más grande que se nos formara, será un Triángulo Rectángulo de 15° y 75° Propiedad Si en un Triángulo Rectángulo si la H ipotenusa es partida en dos por una RECTA que proviene del ángulo de 90°, entonces dicha recta es igual a los lados de la HIPOTENUSA PARTIDA



Triangulos By Romario Kaliman On Emaze




Todo Los Triangulos Notables Sus Angulos Medidas
LUEGO FB =75 EN EL TRIANGULO BEF TENEMOS ANGULOS DE Observando el problema, nos damos cuenta que el Triángulo ABC es un Triangulo Rectángulo, Por ende pasaremos a completar el ángulo que le falta ( 75°) Luego de haber hecho esto nos llevaremos la gran sorpresa que los Triángulos Rectángulos AHB y BHM son iguales ya que tienen un lado en común ( BH ) y dos ángulos iguales ( 15° y 75 ° ) TRIANGULO RECTANGULO NOTABLE DE 15 Y 75 Watch later Share Copy link Info Shopping Tap to unmute wwwgrammarlycom If playback doesn't begin




Hallar A B Triangulos Notables Brainly Lat



2
Triángulo notable de 15° y 75° Podemos caracterizar a un triángulo como notable cuando existe una relación conocida entre sus lados En la mayoría de los casos, las relaciones entre sus lados se limitan a número enteros o número TRIÁNGULOS RECTÁNGULOS NOTABLES DE 30°, 60°, 45°, 37°, 53°




Triangulos Notables Reto Y Ejercicios Propuestos Matemovil



Perimetro De Un Triangulo Rectangulo




Resolucion De Triangulos Superprof




Triangulo Notable De 15 Y 75 6 Youtube



Triangulos Rectangulos Notables
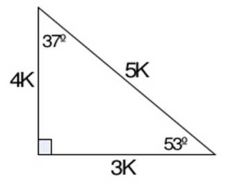



Razones Trigonometricas Notables De Angulos Agudos En Triangulos Rectangulos Articulo Khan Academy




Los Triangulos Rectangulos Notables Y Sus Respectivos Angulos
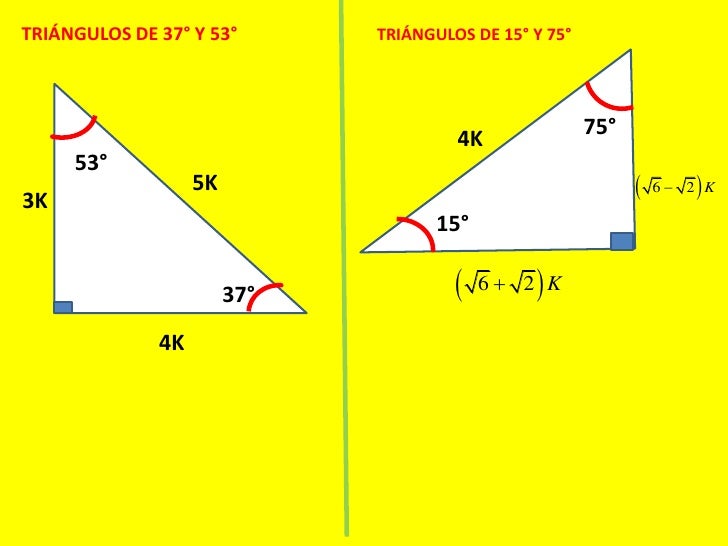



Triangulo Rectangulo



2




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulos Notables




Problemas De Triangulos Notables Para Tercero De Secundaria 21




Todo Los Triangulos Notables Sus Angulos Medidas



Triangulos Notables Recurso Educativo Tiching




Truco Para Las Razones Trigonometricas De Angulos Notables Matematicascercanas
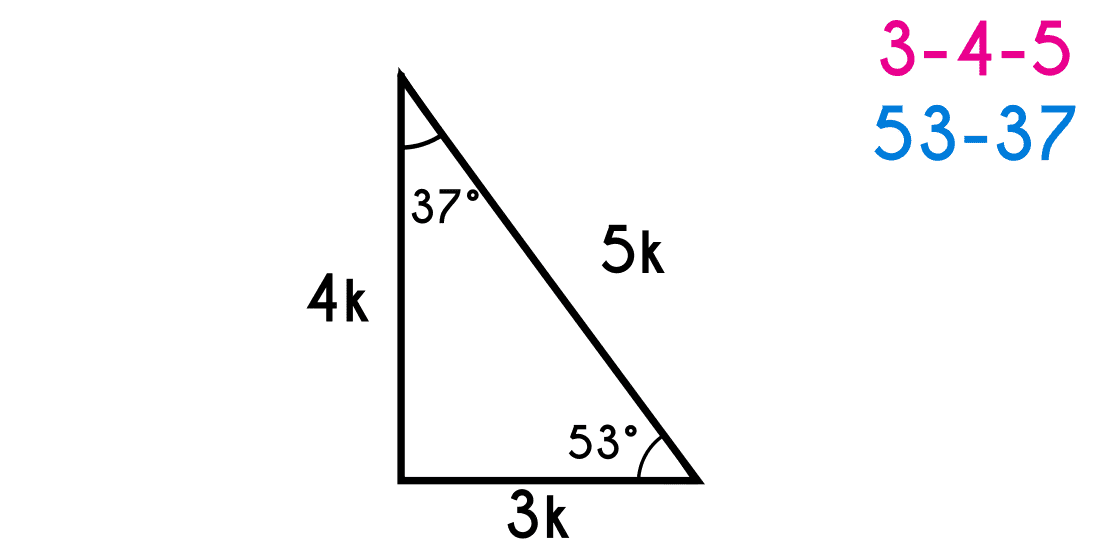



Triangulos Notables Fhybea



Formulas De Los Triangulos Imagui



Deducciones Del Teorema De Pitagoras A Lo Largo De La Historia Como Recurso Didactico En El Proceso De Ensenanza Aprendizaje De La Matematica




Todo Los Triangulos Notables Sus Angulos Medidas




Perimetro De Un Triangulo Rectangulo



2




Triangulos Rectangulos Notables Matemath Web




Trigonometria Problemas De Matematicas Resueltos



2




Triangulo Rectangulo De 75 Y 15 Youtube




Triangulos Rectangulos Notables Y Pitagoricos Para Tercer Grado




Triangulos Rectangulos Notables Matemath Web



Triangulos Notables 15 75



2




Triangulos Rectangulos Notables Completo




Ejercicios Con Triangulos Oblicuangulos Superprof




Todo Los Triangulos Notables Sus Angulos Medidas




Puntos Y Rectas Notables Del Triangulo Matematicascercanas
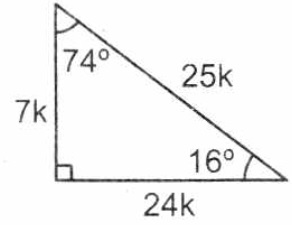



Triangulos Notables By Nicolas Medina By Nicolasmed0123 On Emaze
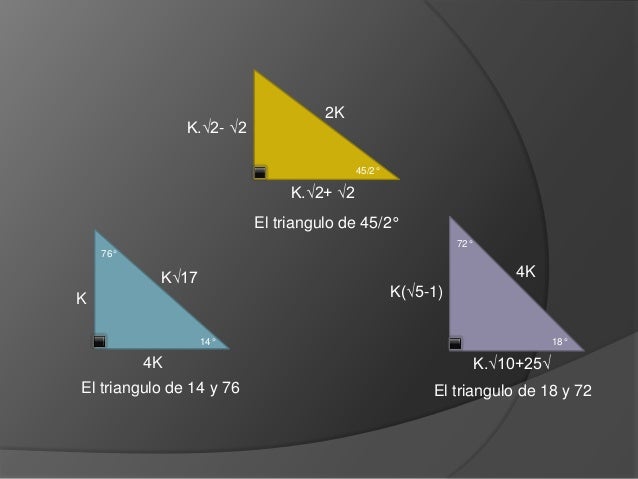



Triangulos Notables




Triangulos Rectangulos Notables Matemath Web
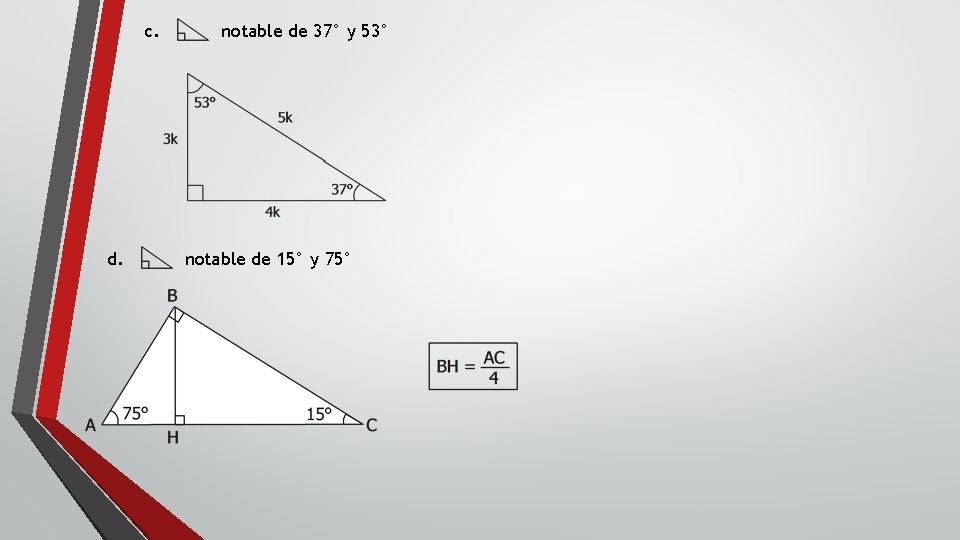



Geometra Captulo 23 Tringulos Rectngulos Notables 1 Er



1




Trigonometria
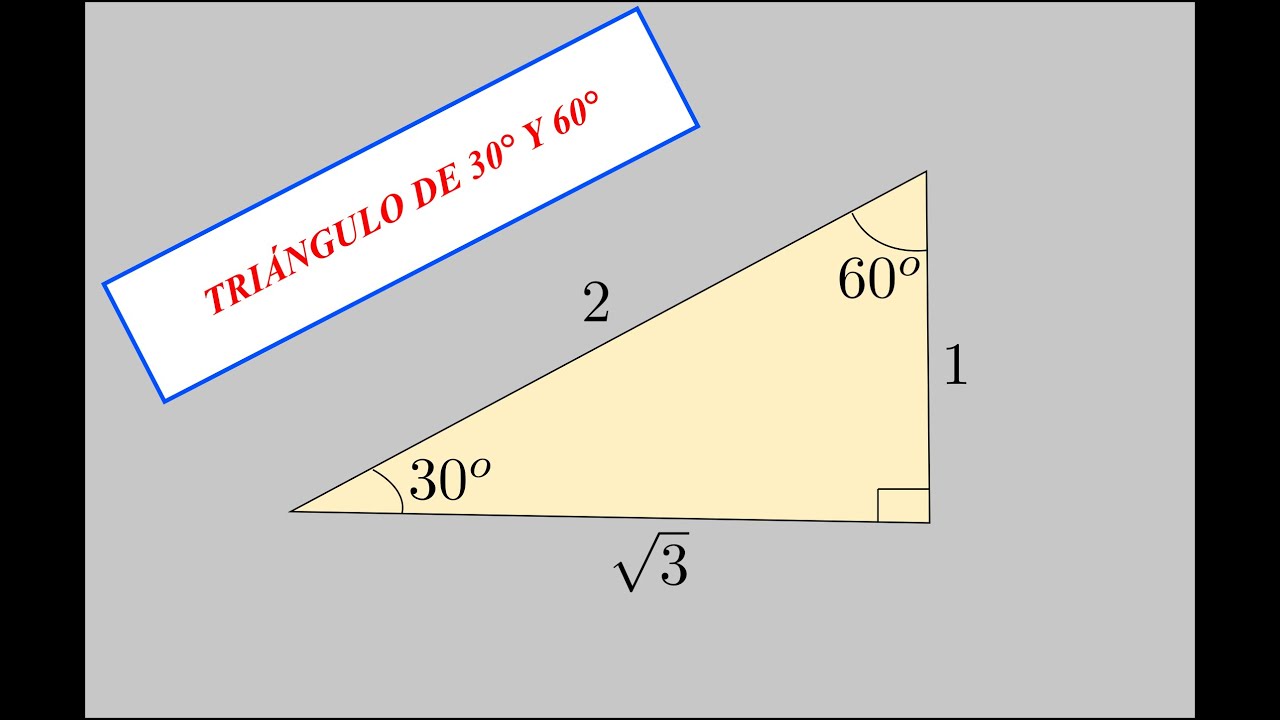



El Triangulo De 15 Y 75 Grados Youtube




Resolucion De Triangulos Superprof




Triangulos Notables Wikipedia La Enciclopedia Libre




3 Triangulos Notables Sistema De Coordenadas Cartesianas Geometria Analitica
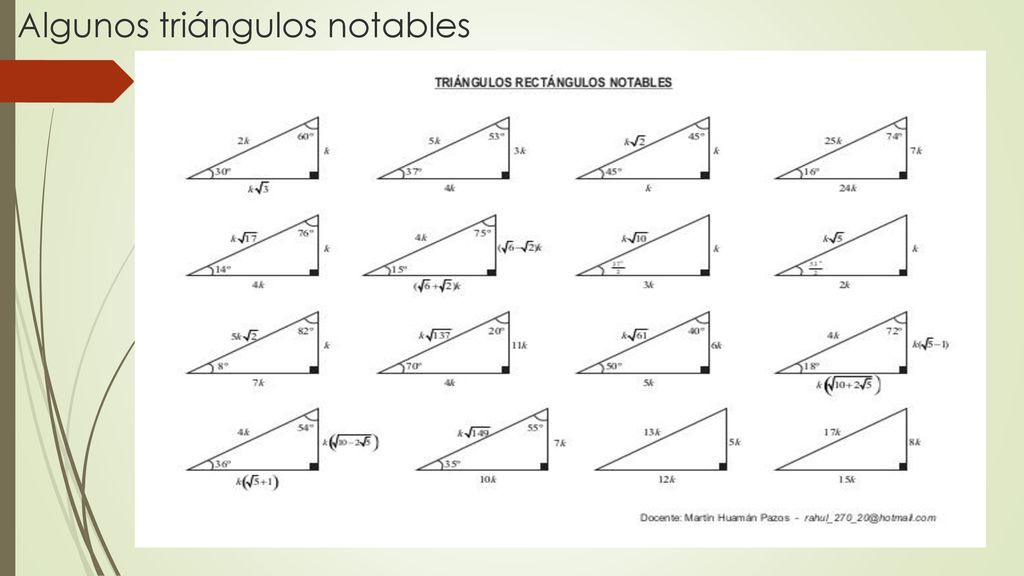



Razones Trigonometricas En El Triangulo Rectangulo Ppt Descargar
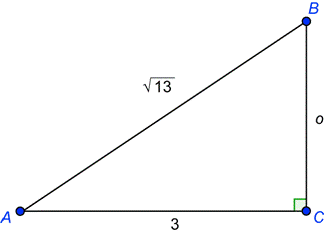



Un Triangulo Rectangulo Tiene Angulos Agudos A Y B Si Y
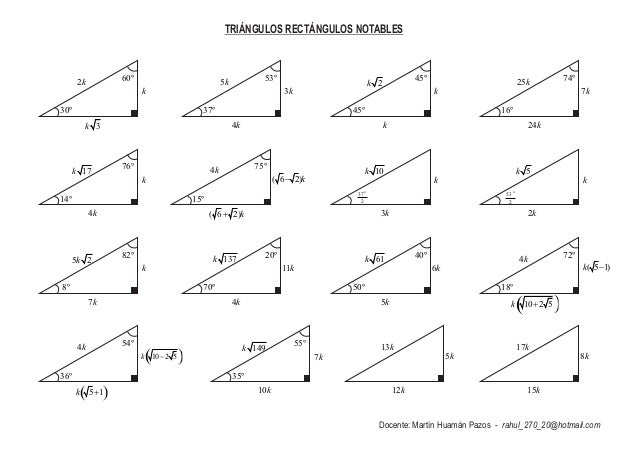



Triangulos Rectangulos Notables Completo




Triangulo Rectangulo Problema 7 Basico




Todo Los Triangulos Notables Sus Angulos Medidas



2




Unidad I Utilicemos Las Razones Trigonometricas Ppt Descargar




Triangulos Notables Estudiandoenlinea
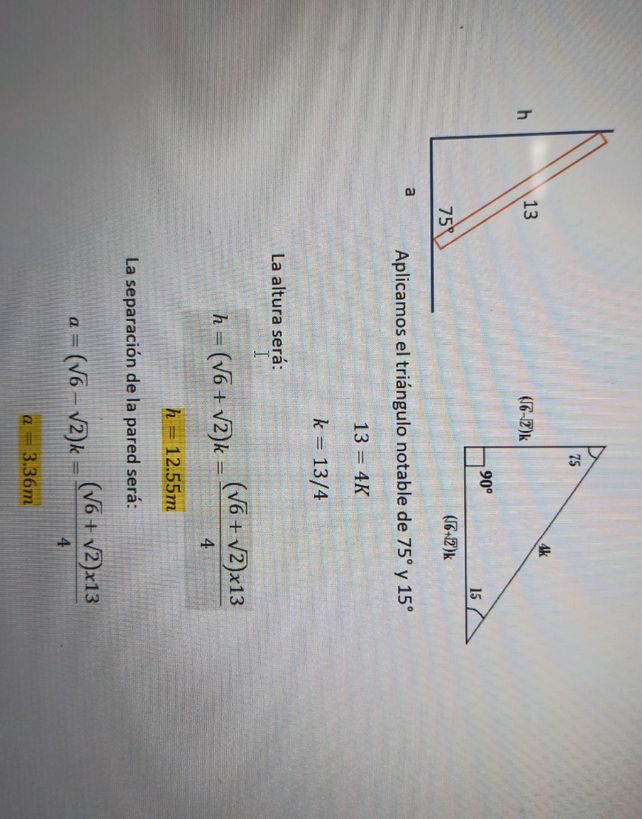



2 Supongamos Que Tenemos Una See How To Solve It At Qanda



Triangulos Notables Reto Y Ejercicios Propuestos Matemovil




Triangulo Rectangulo Notable De 15 Y 75 Youtube



2




Aprender Los 9 Triangulos Rectangulos Notables
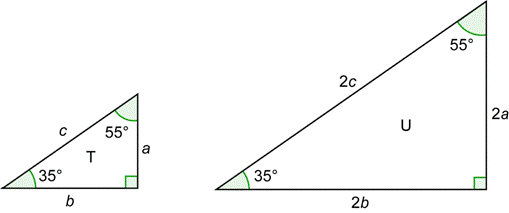



Un Triangulo Rectangulo Tiene Angulos Agudos A Y B Si Y




Triangulos Rectangulos Notables



2




Triangulos Rectangulos Notables Completo




Los Triangulos Rectangulos Notables Y Sus Respectivos Angulos




Calameo Angulos Notables Tabla




Triangulos Rectangulos Notables Matemath Web




El Misterioso Mundo De Las Matematicas Otros Triangulos Notables



Triangulos Notable Matematica Para Secundaria



2




Pin En Problemas
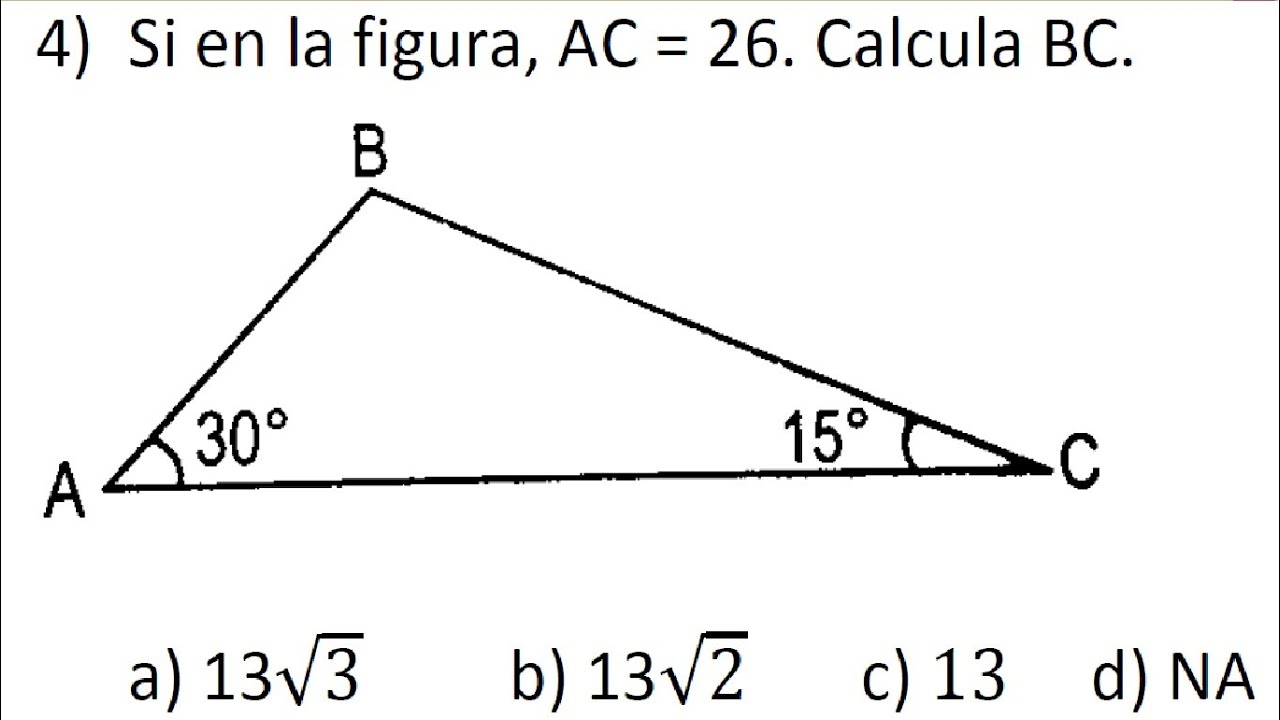



Triangulo Rectangulo Notable 15 Y 75 Youtube




Pin En Libro Logica
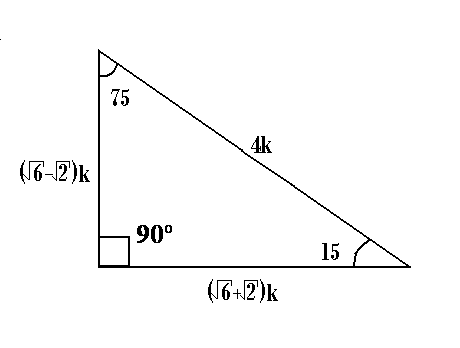



File Triangulo Auxiliar De 75 Y 15 Png Wikimedia Commons




Triangulos Notables Ejercicios Resueltos Pdf




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulo Rectangulo Notable De 15 Y 75 By Fun And Easy




Resolucion De Triangulos Superprof




Triangulos Rectangulos Notables Matemath Web




Geometria Triangulos Ii Brainly Lat



Aekngjyixh2wrm




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulos Notables Reto Y Ejercicios Propuestos Matemovil
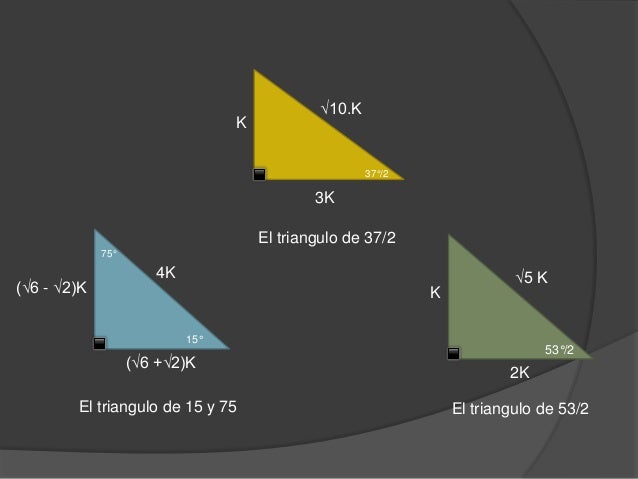



Triangulos Notables



0 件のコメント:
コメントを投稿